Economics, Computer Science, and Policy
Cross-fertilization of ideas and techniques between economics and computer science is yielding fresh insights that can help inform policy decisions.
Perhaps as little as a decade ago, it might have seemed far-fetched for scientists to apply similar methodologies to problems as diverse as vaccination against infectious disease, the eradication of email spam, screening baggage for explosives, and packet forwarding in computer networks. But there are at least two compelling commonalities between these and many other problems. The first is that they can be expressed in a strongly economic or game-theoretic framework. For instance, individuals deciding whether to seek vaccination against a disease may consider how infectious the overall population is, which in turn depends on the vaccination decisions of others. The second commonality is that the problems considered take place over an underlying network structure that may be quite complex and asymmetric. The vulnerability of a party to infectious disease or spam or explosives depends strongly on the party’s interactions with other parties.
The growing importance of network views of scientific and social problems has by now been well documented and even popularized in books such as Malcolm Gladwell’s The Tipping Point, but the central relevance of economic principles in such problems is only beginning to be studied and understood. The interaction between the network and economic approaches to diverse and challenging problems, as well as the impact that this interaction can have on matters of policy, are the subjects I will explore here. And nowhere is this interaction more relevant and actively studied than in the field of computer science.
Research at the intersection of computer science and economics has flourished in recent years and is a source of great interest and excitement for both disciplines. One of the drivers of this exchange has been the realization that many aspects of our most important information networks, such as the Internet, might be better understood, managed, and improved when viewed as economic systems rather than as purely technological ones. Indeed, such networks display all of the properties classically associated with economic behavior, including decentralization, mixtures of competition and cooperation, adaptation, free riding, and tragedies of the commons.
I will begin with simple but compelling examples of economic thought in computer science, including its potential applications to policy issues such as the management of spam. Later, I will argue that the power and scale of the models and algorithms that computer scientists have developed may in turn provide new opportunities for traditional economic modeling.
The economics of computer science
The Internet provides perhaps the richest source of examples of economic inspiration within computer science. These examples range from macroscopic insights about the economic incentives of Internet users and their service providers to very specific game-theoretic models for the behavior of low-level Internet protocols for basic functionality, such as packet routing. Across this entire range, the economic insights often suggest potential solutions to difficult problems.
To elaborate on these insights, let us begin with some background. At practically every level of detail, the Internet exhibits one of the most basic hallmarks of economic systems: decentralization. It is clear that the human users of the Internet are a decentralized population with heterogeneous needs, interests, and incentives. What is less widely known is that the same statement applies to the organizations that build, manage, and maintain what we call monolithically the Internet. In addition to being physically distributed, the Internet is a loose and continually changing amalgamation of administratively and economically distinct and disparate subnetworks (often called autonomous systems). These subnetworks vary dramatically in size and may be operated by institutions that simply need to provide local connectivity (such as the autonomous system administered by the University of Pennsylvania), or they may be in the business of providing services at a profit (such as large backbone providers like AT&T). There is great potential for insight from studying the potentially competing economic incentives of these autonomous systems and their users. Indeed, formal contractual and financial agreements between different autonomous systems specifying their connectivity, exchange of data and pricing, and other interactions are common.
Against this backdrop of decentralized administration, a number of prominent researchers have posited that many of the most common problems associated with the Internet, such as email spam, viruses, and denial-of-service attacks, are fundamentally economic problems at their core. They may be made possible by networking technology, and one may look for technological solutions, but it is often more effective to attack these problems at their economic roots.
For example, many observers argue that problems such as spam would be best addressed upstream in the network. They contend that it is more efficient to have Internet service providers (ISPs) filter spam from legitimate mail, rather than to have every end user install spam protection. But such purely technological observations ignore the question of whether the ISPs have an economic incentive to address such problems. Indeed, it has been noted that some ISPs have contractual arrangements with their corporate customers that charge fees based on the volume of data carried to and from the customer. Thus, in principle, an ISP could view spam or a denial-of-service attack as a source of potential revenue.
An economic view of the same problem is that spam has proliferated because the creation of a nearly free public resource (electronic mail) whose usage is unlimited has resulted in a favorable return on investment for email marketing, even under infinitesimal take rates for the products or services offered. One approach is to accept this economic condition and pursue technological defenses such as spam filters or whitelists and blacklists of email addresses. An alternative is to seek to alter the economic equation that makes spam profitable in the first place, by charging a fee for each email sent. The charge should be sufficiently small that email remains a nearly free resource (aside from Internet access costs) for nearly all non-spammers, but sufficiently large to eradicate or greatly reduce the spammer’s profitability. There are many challenging issues to be worked out in any such scheme, including who is to be paid and how to aggregate all the so-called micropayments. But the mere fact that computer scientists are now incorporating real-world economics directly into their solutions or policy considerations represents a significant shift in their view of technology and its management.
As an example of economic thought at the level of the Internet’s underlying protocols, consider the problem of routing, the multi-hop transmission of data packets across the network. Although a delay of a second or two is unimportant for email and many other Internet operations, it can be a serious problem for applications such as teleconferencing and Internet telephony, where any latency in transmission severely degrades usefulness. For these applications, the goal is not simply to move data from point A to point B in the Internet, but to find the fastest possible route among the innumerable possible paths through the distributed network. Of course, which route is the fastest is not static. The speed of electronic traffic, like the speed of road traffic, depends on how much other traffic is taking the same route, and the electronic routes can be similarly disrupted by “accidents” in the form of temporary outages or failures of links.
Recently, computer scientists have begun to consider this problem from a game-theoretic perspective. In this formulation, one regards a network user (whether human or software) as a player in a large-population game in which the goal is to route data from one point to another in the network. There are many possible paths between the source and destination points, and these different paths constitute the choice of actions available to the player. Being “rational” in this context means choosing the path that minimizes the latency suffered in routing the data. A series of striking recent mathematical results has established that the “price of anarchy”— a measure of how much worse the overall latency can be at competitive equilibrium in comparison to the best “socialist” or centrally mandated nonequilibrium choice of routes—is surprisingly small under certain conditions. In other words, in many cases there is not much improvement in network behavior to be had from even the most laborious centralized network design. In addition to their descriptive properties, such results also have policy implications. For example, a number of plausible schemes for levying taxes on transmission over congested links of the network have been shown to significantly reduce the price of anarchy.
These examples are just some of the many cases of computer scientists using the insights of economics to solve problems. Others include the study of electronic commerce and the analysis and design of complex digital markets and auctions.
The computer science of economics
The flow of ideas between computer science and economics is traveling in both directions, as some economists have begun to apply the insights and methods of computer science to new and old problems. The computer scientist’s interest in economics has been accompanied by an explosion of research on algorithmic issues in economic modeling, due in large part to the fact that the economic models being entertained in computer science are often of extraordinarily large dimension. In the game-theoretic routing example discussed above, the number of players equals the number of network users, and the number of actions equals the number of routes through the network. Representing such models in the so-called normal form of traditional game theory (where one explicitly enumerates all the possibilities) is infeasible. In recent years, computer scientists have been examining new ways of representing or encoding such high-dimensional models.
Such new encodings are of little value unless there are attendant algorithms that can manipulate them efficiently (for instance, performing equilibrium and related computations). Although the computational complexity of certain basic problems remains unresolved, great strides have been made in the development of fast algorithms for many high-dimensional economic models. In short, it appears that from a computational perspective, many aspects of economic and game-theoretic modeling may be ready to scale up. We can now undertake the construction and algorithmic manipulation of numerical economic models whose complexity greatly exceeds those one could have contemplated a decade ago.
Finally, it also turns out that the analytical and mathematical methods of computer science are extremely well suited to examining the ways in which the structure of an economic model might influence the expected outcomes in the models; for instance, the way in which the topology of a routing network might influence the congestion experienced at game-theoretic equilibrium, the way in which the connectivity pattern of a goods exchange network might influence the variation in prices or the distribution of wealth, or (as we shall see shortly) the way in which transfers of passengers between air carriers might influence their investment decisions for improved security.
Interdependence in computer security
To illustrate some of these computational trends, I will examine a case study drawn from my own work on a class of economic models known as interdependent security (IDS) games, which nicely capture a wide range of commonly occurring risk management scenarios. Howard Kunreuther of the Wharton School at the University of Pennsylvania and Geoffrey Heal of Columbia University introduced the notion of IDS games, which are meant to capture settings in which decisions to invest in risk mitigation may be heavily influenced by natural notions of risk “contagion.” Interestingly, this class is sufficiently general that it models problems in areas as diverse as infectious disease vaccination, corporate compliance, computer network security, investment in research, and airline baggage screening. It also presents nontrivial computational challenges.
Let us introduce the IDS model with another example from computer science, the problem of securing a shared computer resource. Suppose you have a desktop computer with its own software and memory, but you also keep your largest and most important data files on a hard disk drive that is shared with many other users. Your primary security concern is thus that a virus or other piece of malicious software might erase the contents of this shared hard drive. Your desktop computer and its contents, including all of your email, any programs or files you download, and so on, is a potential point of entry for such “malware,’’ but of course so are the desktop machines of all the other users of the hard disk.
Now imagine that you face the decision of whether to download the most recent updates to your standard desktop security software, such as Norton Anti-Virus. This is a distinct investment decision; not so much because of the monetary cost but because it takes time and energy for you to perform the update. If your diligence were the only factor in protecting the valued hard drive, your incentive to suffer the hassle would be high. But it is not the only factor. The safety of the hard drive is dependent on the diligence of all of the users whose desktop machines present potential points of compromise, since laziness on the part of just a single user could result in the breach that wipes the disk clean forever. Furthermore, some of those users may not keep any important files on the drive and therefore have considerably less concern than you about the drive’s safety.
Thus, your incentive to invest is highly interdependent with the actions of the other players in this game. In particular, if there are many users, and essentially none of them are currently keeping their security software updated, your diligence would have at best an incremental effect on an already highly vulnerable disk, and it will not be worth your time to update your security software. At the other extreme, if the others are reliable in their security updates, your negligence would constitute the primary source of vulnerability, so you can have a first-order effect on the disk’s safety by investing in the virus updates.
Kunreuther and Heal propose a game-theoretic model for this and many other related problems. Although the formal mathematical details of this model are beyond our current scope, the main features are as follows:
- Each player (such as the disk users above) in the game has an investment decision (such as downloading security updates) to make. The investment can marginally reduce the risk of a catastrophic event (such as the erasure of the disk).
- Each player’s risk can be decomposed into direct and indirect sources. The direct risk is that which arises because of a players own actions or inactions, and it can be reduced or eradicated by sufficient investment. The indirect risk is entirely in the hands of the rest of the player population. In the current example, your direct risk is the risk that the disk will be erased by malware entering the system through your own desktop machine. Your remaining risk is the indirect risk that the disk will be erased by malware entering through someone else’s machine. You can reduce the former by doing the updates, but you can do nothing about the latter.
- Rational players will choose to invest according to the tradeoff presented by the two sources of risk. In the current example, you would choose to invest the least update effort when all other parties are negligent (since the disk is so vulnerable already that there is little help you alone can provide) and the most when all other parties are diligent (since you constitute the primary source of risk).
- The predicted outcomes of the IDS model are the (Nash) equilibria that can arise when all players are rational; that is, the collective investment decisions in which no player can benefit by unilateral deviation. In such an equilibrium, every party is optimizing their behavior according to their own cost/benefit tradeoff and the behavior of the rest of the population.
Baggage screening unraveled
In the shared disk example, there is no interesting network structure per se, in the sense that users interact with each other solely through a shared resource, and the effect of any given user is the same on all other users: By being negligent, you reduce the security of the disk by the same amount for everyone, not differentially for different parties. In other words, there are no network asymmetries: All pairs of parties have the same interactions, even though specific individuals may influence the overall outcome differently by their different behaviors.
Kunreuther and Heal naturally first examined settings in which such asymmetries are absent, so that all parties have the same direct and indirect risks. Such models permit not only efficient computation but even the creation of simple formulas for the possible equilibria. But in more realistic settings, asymmetries among the parties will abound, precluding simple characterizations and presenting significant computational challenges. It is exactly in such problems that the interests and strengths of computer science take hold.
A practical numerical and computational example of IDS was studied in recent work done in my group. In this example, the players are air carriers, the investment decision pertains to the amount of resources devoted to luggage screening for explosives, the catastrophic event is a midair explosion, and the network structure arises from baggage transfers between pairs of carriers.
Before describing our experiments, I provide some background. In the United States, individual air carriers determine the procedures and investments they each make in baggage screening for explosives and other contraband, subject to meeting minimum federal requirements. Individual bags are thus subjected to the procedures of whichever carrier a traveler boards at the beginning of a trip. If a bag is transferred from one carrier to another, the receiving carrier does not rescreen according to its own procedures but simply accepts the implicit validation of the first carrier. The reasons for this have primarily to do with efficiency and the cost of repeated screenings. The fact that carriers are free to apply procedures that exceed the federal requirements is witnessed by the practices of El Al Airlines, which is also an exception in that it does in fact screen transferred bags.
As in the shared disk example, there is thus a clear interdependent component to the problem of baggage screening. If a carrier receives a great volume of transfers from other carriers with lax security, it may actually have little incentive to invest in improved security for the bags it screens directly: The explosion risk presented by the transferred bags is already so high that the expense of the marginal improvement in direct check security is unjustified. (Note: For simplicity, I am not considering the expensive proposition of rescreening transferred bags, but only of improving security on directly checked luggage.) Alternatively, if the other airlines maintain extremely high screening standards, a less secure carrier’s main source of risk may be its own checked baggage, creating the incentive for improved screening. Kunreuther and Heal discuss how the fatal explosion aboard Pan Am flight 103 over Lockerbie, Scotland, in 1988 can be viewed as a deliberate exploitation of the interdependent risks of baggage screening.
The network structure in this case arises from the fact that there is true pairwise interaction between carriers (as opposed to the shared disk setting, where all interactions were indirect and occurred via the shared resource). Since not all pairs of airlines may transfer bags with each other, or may not do so in equal volume, strong asymmetries may emerge. Within the same network of transfers, some airlines may find themselves receiving many transfers from carriers with lax security, and others may receive transfers primarily from more responsible parties. On a global scale, one can imagine that such asymmetries might arise from political or regulatory practices in different geographical regions, demographic factors, and many other sources. Such a network structure might be expected to have a strong influence on outcomes, since the asymmetries in transfers will create asymmetries of incentives and therefore of behavior.
In the work of my group, we conducted the first large-scale computational and simulation study of IDS games. This simulation was based on a data set containing 35,362 records of actual civilian commercial flight reservations (both domestic and international) made on August 26, 2002. Each record contains a complete flight itinerary for a single individual and thus documents passenger (and therefore presumably baggage) transfers between the 122 commercial air carriers appearing in the data set. The data set contained no identifying information for individuals. Furthermore, since I am describing an idealized simulation based on limited data, I will not identify specific carriers in the ensuing discussion.
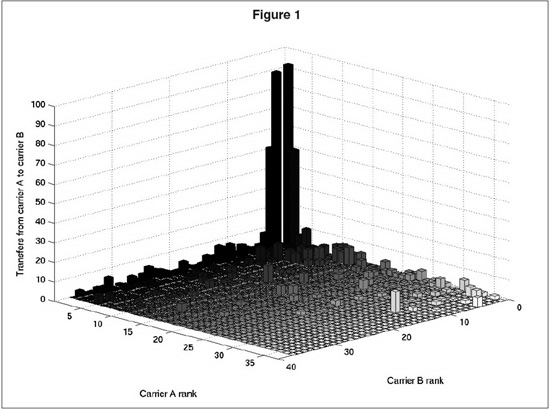
I will begin by discussing the raw data itself—in particular, the counts of transfers between carriers. Figure 1 shows a visualization of the transfer counts between the 36 busiest carriers (as measured by the total flight legs on the carrier appearing in the data). Along each of the horizontal axes, the carriers are arranged in order of number of flight legs (with rank 1 being the busiest carrier, and rank 36 the least). At each grid cell, the vertical bar shows the number of transfers from one particular carrier to another. Thus, transfers between pairs of the busiest (highest-rank) carriers appear at the far corner of the diagram; transfers between pairs of the least busy carriers in the near corner; and so on.
Despite its simplicity, Figure 1 already reveals a fair amount of interesting structure in the (weighted) network of transfers between the major carriers. Perhaps the most striking property is that an overwhelming fraction of the transfers occur among the handful of largest carriers. This is visually demonstrated by the “skyscrapers” in the far corner, which dominate the landscape of transfers.
Scientists and travelers know that the hub and spoke system of U.S. airports naturally leads to a so-called “heavy-tailed” distribution of flights in which a small number of major airports serve many times the volume of the average airport. Here we are witnessing a similar phenomenon across air carriers rather than airports: The major carriers account for almost all the volume, as well as almost all the transfers. This is yet another example of the staggering variety of networks—transportation, social, economic, technological, and biological—that have been demonstrated in recent years to have heavy-tailed properties of one kind of another. Beyond such descriptive observations, less is known about how such properties influence outcomes. In a moment, we will see the profound effect that the imbalanced structure of the carrier transfer network has on the outcome predicted by our IDS simulation, and how simple models can suggest how such structure can lead rather directly to policy suggestions.
In order to perform the simulations, the empirical number of transfers in the data set from carrier A to carrier B was used to set a parameter in the IDS model that represents the probability of transfer from A to B. The numerical IDS model that results does not fall into any of the known classes for which the computation of equilibria can be performed efficiently. However, this is not a proof of intractability, because we are concerned here with a specific model and not general classes. We thus performed simulations on the numerical model in which each carrier gradually adapts its investment behavior in response to its current payoff for investment, which depends strongly on the current investment decisions of its network neighbors in the manner we have informally described. (See the “IDS Models” at the end for a detailed explanation of the model.)
The most basic question about such a simulation is whether it converges to a predicted equilibrium outcome. There is no a priori reason why it must, since the independent adaptations of the carriers could, for instance, result in cyclical investment behavior. This question is easily answered: The simulation quickly converges to an equilibrium, as do all of the many variants we examined. This is a demonstration of a common phenomenon in computer science: the empirical effectiveness of a heuristic on a specific instance of a problem that may be computationally difficult in general. Further, it is worth noting that the particular heuristic here—the gradual adaptation of investment starting from none—is more realistic than a “black-box” equilibrium outcome that identifies only the final state, because it suggests the dynamic path by which the carriers might actually arrive at equilibrium starting from natural initial conditions.
The more interesting question, to which we now turn, is what are the properties of the predicted equilibrium? And if we do not like those properties, what might we do about it?
The answer, please
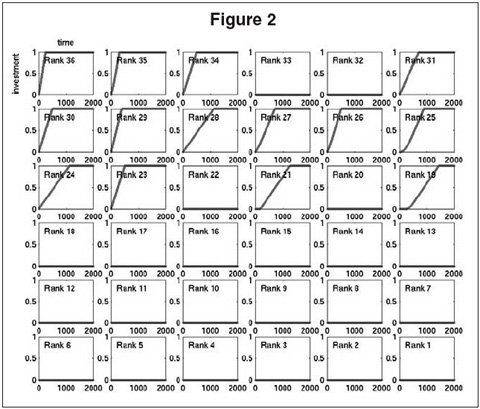
Figure 2 shows the results of the simulation described above. The figure shows a 6-by-6 grid of 36 plots, one for each of the 36 busiest (again, according to overall flight traffic in the data set) out of the 122 carriers. The plot in the upper left corner corresponds to the 36th busiest carrier, and the plot in the lower right corner corresponds to the busiest. The x axis of each plot corresponds to time in units of simulation steps, and the y axis shows the level of investment between 0 (no investment) and 1 (the hypothetical maximum investment) for the corresponding carrier as it adapts during the simulation. As noted above, all carriers start out at zero investment.
Examining the details of Figure 2, we find that within approximately 1,500 steps of simulation, the population of carriers has converged to an equilibrium and no further adaptation is taking place; carrier 18 is the last to converge. From the viewpoint of societal benefit, the outcome we would prefer to emerge is that in which all carriers fully invest in improved screening. Instead, the carriers converge to a mixture of those who invest fully and those who invest nothing. In general, this mixture obeys the ordering by traffic volume: The less busy carriers tend to converge to full investment, whereas the larger carriers never move from their initial position of no investment. This is due to the fact that, according to the numerical model, the larger carriers generally face a large amount of indirect or transfer risk and thus have no incentive to improve their own screening procedures. Smaller carriers can better control their own fate with improved screening, since they have fewer transferred bags. There are exceptions to this simple ordering. For instance, the carriers of rank 32 and 33 do not invest despite the fact that carriers with similar volume choose to invest. These exceptions are due to the specific transfer parameters of the carriers. The carriers of rank 37 to 122 (not shown) all converge to full investment.
Figure 2 thus shows that the price of anarchy in our numerical IDS baggage screening model is quite high: The outcome obtained by letting carriers behave independently and selfishly is far from the desired societal optimum of full investment. The fact that “only” 22 of the 122 carriers converge to no investment is little consolation given the fact that they include all the largest carriers, which account for the overwhelming volume of flights. The model thus predicts that an insecure screening system will arise from the interdependent risks.
Even more interesting than this baseline prediction are the policy implications that can derived by manipulation of the model. One way of achieving the desired outcome of full investment by all carriers would be for the federal government to subsidize all carriers for improved security screening. A natural economic question is whether the same effect can be accomplished with minimal centralized intervention or subsidization.
Figure 3 shows the results of one such thought experiment. The format of the figure is identical to that of Figure 2, but one small and important detail in the simulation was changed. In the simulation depicted in Figure 3, the two largest carriers have had their investment levels fixed at the maximum of 1, and they are not adapted from this value during the simulation. In other words, we are effectively running an experiment in which we have subsidized only the two largest carriers.
The predicted effects of this limited subsidization are quite dramatic. Most notably, all of the remaining carriers now evolve to the desired equilibrium of full investment. In other words, the relatively minor subsidization of two carriers has created the economic incentive for all other carriers to invest in improved security. This is an instance of the tipping phenomenon first identified by Thomas Schelling and recently popularized by Malcolm Gladwell: a case in which a behavioral change by a small collection of individuals causes a massive shift in the overall population behavior.
Figure 3 also nicely demonstrates cascading behavior among the non-subsidized carriers. The subsidization of the two largest carriers does not immediately cause all carriers to begin investing from the start of the simulation. Rather, some carriers (again mainly the larger ones) begin to invest only once a sufficient fraction of the population has invested enough to make their direct risk primary and their transfer risk secondary. Indeed, the seventh largest carrier has an economic incentive to invest only toward the end of the simulation and is the last to converge. This cascading effect, in which the tipping phenomenon occurs sequentially in a distinct order of investment, was present in the original simulation but is much more pronounced here.
Of course, the two largest carriers form only one tipping set. There may be other collections of carriers whose coerced investment, either through subsidization or other means, will cause others to follow. Depending on more detailed economic assumptions we can make about the investment in question, some tipping sets may be more or less expensive to implement than others. Natural policy questions include asking what the most cost-effective and practical means of inducing full investment are, and such models facilitate the exploration of a large number of alternative answers.
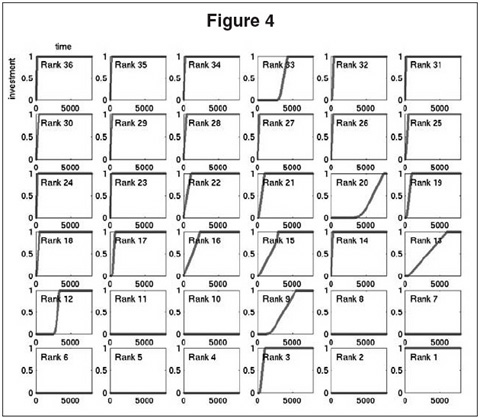
The model can also predict necessary conditions for tipping. In Figure 4, we show the results of the simulation in which only the largest carrier is subsidized. Although this has salutary effects, stimulating investment by a number of carriers (such as carrier 3) that would not otherwise have invested, it is not sufficient to cause the entire population to invest. The price of anarchy remains high, with most of the largest carriers not investing. As a more extreme negative example, we found that subsidizing all but the two largest of the 122 carriers is still insufficient to induce the two largest to invest anything; the highly interdependent transfer risk between just these two precludes one of them investing without the other.
What next?
The IDS case study examined above is only one example in which a high-dimensional network structure, an economic model, computational issues, and policy interact in an interesting and potentially powerful fashion. Others are beginning to emerge as the dialogue between computer scientists and economists heats up. For instance, in my group we have also been examining high-dimensional network versions of classical exchange models from mathematical economics, such as those studied by Kenneth Arrow and Gerard Debreu. In the original models, consumers have endowments of commodities or goods and utility functions describing their preferred goods; exchange takes place when consumers trade their endowments for more preferred goods. In the variants we have studied, there is also an underlying network structure defining allowable trade: Consumers are allowed to engage in trade only with their immediate neighbors in the network.
The introduction of such natural restrictions on the models radically alters basic properties of their price equilibria. The same good can vary in price across the economy due entirely to network asymmetries, and individual consumers may be relatively economically advantaged or disadvantaged by the details of their position in the overall network. In addition to being an area that has seen great strides in efficient algorithms for equilibrium computation, it is also one that again highlights the insights that computer science can bring to the relationship between structure and outcome. For example, it turns out that a long-studied structural property of networks known in computer science as “expansion” offers a characterization of which networks will have no variation in prices and which will have a great deal of variation. Interestingly, expansion properties are also closely related to the theory of random walks in networks. The intuition is that if, when randomly wandering around a network, there are regions where one can become stuck for long periods, these same regions are those where economic imbalances such as price variation and low wealth can emerge. Thus, there is a direct relationship between structural and economic notions of isolation.
We have also performed large-scale numerical experiments on similar models derived from United Nations foreign exchange data. Such experiments demonstrate the economic power derived purely from a nation’s position in an idealized network structure extracted from the data. The models and algorithms again support thought-provoking predictive manipulations. For instance, in the original network we extracted, the United States commanded the highest prices at equilibrium by a wide margin. When the network was modified to model a truly unified, frictionless European Union, the EU instead became the predicted economic superpower.
Looking forward, the research dialogue between the computer science and economics communities is perhaps the easy part, since they largely share a common mathematical language. More difficult will be convincing policymakers that this dialogue can make more than peripheral contributions to their work. For this to occur, the scientists will need to pick their applications carefully and to work hard to understand the constraints on policymakers in those arenas. This sociological step, when scientists wade into the often messy waters where their methods must prove useful despite political, budgetary, and other constraints, is not likely to be easy. But it seems that the time for the attempt has arrived, since the computational, predictive, and analytical tools for considerably more ambitious economic models are quickly falling into place.
As I have discussed, within computer science the influence of economic models is already beginning to inform policy. This is a particularly favorable domain, since so many of the policy issues have technology at their core; the scientists and policy-makers are often close or even the same individuals. Similarly promising areas include epidemiology and transportation, the latter including topics such as our application of IDS to baggage screening. That case study exemplifies both the opportunities and challenges. It provides compelling but greatly oversimplified evidence for the potential policy implications of rich models. The missing details—the specifics of plausible security screening investments, the metrics of the carriers’ direct risks based on demographics and history, and many others—must be filled in for the model to be taken seriously. But regardless of the domain, all that is required to start is a scientist and a policymaker ready to work together in a modern and unusual manner.
IDS Models and Their Computational Challenges
When one formalizes the IDS baggage screening problem, the result is a model for the payoffs of a game determined by the following parameters:
I. For each carrier A, a numerical parameter D(A),quantifying the level of the direct risk of A; intuitively, the probability that this particular carrier directly checks a bag containing an explosive onto a flight. Obviously, this parameter might vary from carrier to carrier, depending (among other things) on the ambient level of risk presented by the demographics of its customer base or the geographic region of the carrier.
II. For each pair of carriers A and B, a numerical paramater T(A,B), quantifying the indirect risk that A faces due to transferred bags from B; intuitively, the probability that a bag transferred from a flight of B to a flight of A contains an explosive device. This parameter might vary for different carrier pairs, depending (among other things) on the volume of transfers from B to A and the direct risk of B.
III. Parameters, possibly varying from carrier toticated carrier, quantifying the required investment I(A) for improved screening technology or procedures and the cost E(A) of an in-flight explosion.
The resulting multiparty game is described by a payoff function for each carrier A that will depend on E(A), I(A), D(A), and the parameters T(A,B) for all other carriers B.
For the numerical experiments we describe, the empirical number of transfers in the data set from carrier B to carrier A was used to set the parameter T(A,B). Note that despite the large number of records in the data set, it is actually rather small compared to the number of pairs of carriers, thus leading to many transfer counts that are zero. However, our simulation results appear robust even when standard forms of “smoothing” are applied to these sparse estimates.
Although the data set contains detailed empirical evidence on intracarrier transfers, it provides no guidance on the setting of the other IDS model parameters (for direct risks and for investment and explosion costs). These were thus set to common default values for the simulations. In future work, they could clearly be replaced by either human estimates or a variety of sources of data. For instance, direct risks could be derived from statistics regarding security breaches at the individual carriers or at the airports where they receive the greatest direct-checked volume. Let us briefly delve into the computational challenges presented by such models. The sheer number of parameters is dominated by those in category II. There is one such parameter per pair of carriers, so the number of parameters in this category grows roughly with the square of the number of carriers. For instance, in our model with over 100 carriers, the number of parameters of the model already exceeds 10,000. We are thus interested in algorithmically manipulating rather high-dimensional models.
From the theoretical standpoint, the computationalnews on such models is mixed, but in an interestingrameter way. If we consider the completely general case given by parameter categories I, II, and III above, it is possible to prove formally that in the worst case, there may be certain equilibria that are computationally intractable to find. On the other hand, various restrictions on or assumptions about the parameters (particularly the transferdirect parameters in category II) allow one to develop sophisticated algorithms that can efficiently compute all of the possible outcomes. Such mixed results—in which theproved most ambitious variant of the problem is computationally infeasible, but in which nontrivial algorithms can tackle nontrivial special cases—is often a sign of an interesting problem in computer science.
Of course, the real world also typically lies somewhere in between the provably solvable and worst cases. And one often finds that simple and natural heuristics can be surprisingly effective and yield valuable insights. In particular, in the simulations we describe, an heuristic known as gradient descent was employed. More precisely, according to the IDS model, the numerical payoff that carrier A will receive from investment in improved screening depends on the current investments of the other carriers, weighted by their probability of transferring passengers to carrier A. This payoff could be either positive (incentive for increased investment) or negative (disincentive for increased investment). In our simulations, carrier A simply incrementally adjusts its current investment up or down according to this incentive signal, and all other carriers do likewise. All carriers begin with no investment, and we assume that there is a maximum possible investment of 1. Such gradient approaches to challenging computational problems are common in the sciences. There are many possible natural variants of this simulation that can be imagined.